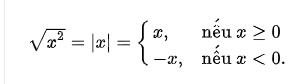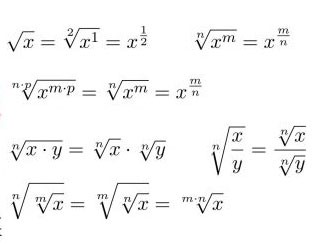La radice quadrata è una delle conoscenze matematiche più importanti, utilizzata durante tutto il processo di apprendimento degli studenti. Nel seguente articolo spiegheremo cos'è una radice quadrata e come calcolare la radice quadrata di un numero. Fare riferimento a.
Sommario
Cos'è la radice quadrata?
La radice quadrata di un numero a è un numero x tale che x2 = a, o in altre parole, il numero x il cui valore al quadrato = a.
Ad esempio, 2 e −2 sono radici quadrate di 2 perché 2² = (−2)² = 4.
Il segno di radice è indicato con √.
- Ogni numero reale non negativo a ha un'unica radice quadrata non negativa, chiamata radice quadratica aritmetica.
Ad esempio, la radice quadrata aritmetica di 16 è 4, indicata con √16 = 4, perché 4² = 4 × 4 = 16 e 4 è un numero non negativo.
Ogni numero positivo a ha due radici quadrate: √a è una radice quadrata positiva e −√a è una radice quadrata negativa. Sono indicati simultaneamente come ± √a.
I calcoli più basilari della radice quadrata
Ricorda alcuni numeri quadrati di base e più comuni, così quando estrarrai le radici quadrate potrai calcolare più velocemente a mente:
0² = 0
1² = 1
3² = 9
4² = 16
5² = 25 6² = 36
7² = 49
8² = 64
9² =
81 10² =
100
11² = 121 12²
= 144
13² = 169
14² = 196
15² = 225
16² = 256
17² = 289
Alcune formule di base per l'estrazione della radice quadrata che tutti dovrebbero ricordare sono:
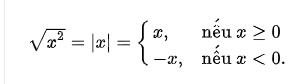
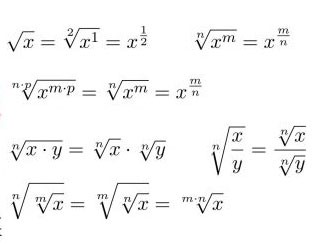
Tabella delle radici quadrate
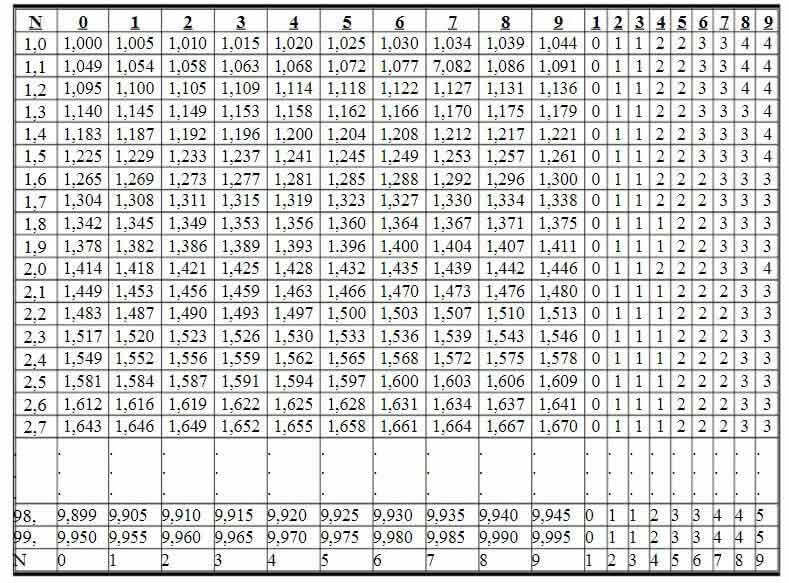
La tabella delle radici quadrate è divisa in righe e colonne, consentendo di trovare direttamente la radice quadrata dei numeri maggiori di 1 e minori di 100.
Le radici quadrate dei numeri scritti con non più di tre cifre da 1,00 a 99,9 sono riportate nella tabella nelle colonne da 0 a 9. Seguono nove colonne di correzione utilizzate per correggere l'ultima cifra delle radici quadrate dei numeri scritti con quattro cifre da 1,000 a 99,99.
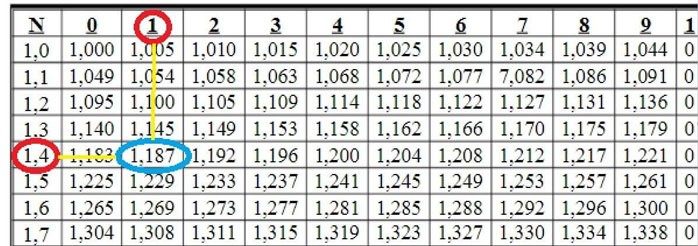
Esempio 1: Trova
→ Soluzione:
All'intersezione delle righe 1,4 e della colonna 1 vediamo il numero 1.187
COSÌ
Esempio 2:
Trovare
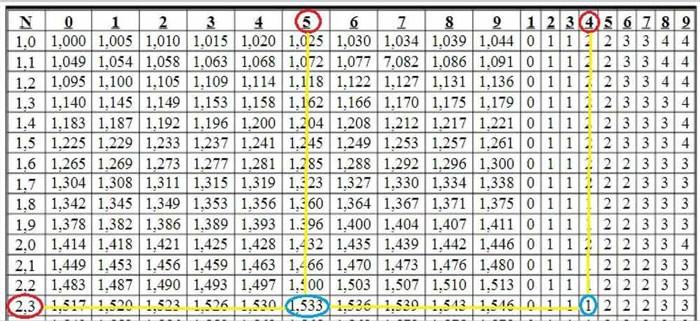
All'intersezione delle righe 2, 3 e della colonna 5 vediamo il numero 1,533. Abbiamo
Successivamente, all'intersezione delle righe 2, 3 e della colonna 4, vediamo il numero 1. Questo numero 1 viene utilizzato per correggere l'ultima cifra del numero. Cioè: 1,533 + 0,001 = 1,534
COSÌ
Come calcolare la radice quadrata senza usare la calcolatrice
Trova la radice quadrata di un numero intero
Trova la radice quadrata tramite la moltiplicazione.
La radice quadrata di un numero è il numero che, moltiplicato per se stesso, dà il numero originale.
Quindi questo significa "Quale numero puoi moltiplicare per se stesso per ottenere il numero che hai già?"
Per esempio:
La radice quadrata di 1 è 1 perché 1 per 1 è uguale a 1 (1 X 1 = 1).
La radice quadrata di 4 è 2 perché 2 per 2 è uguale a 4 (2 X 2 = 4).
La radice quadrata di 9 è 3 perché 3 x 3 = 9.
Utilizzare la divisione per trovare la radice quadrata
Per trovare la radice quadrata di un numero intero, puoi dividere il numero intero per numeri successivi fino a trovare un quoziente che sia esattamente uguale al divisore.
Per esempio:
16 diviso 4 fa 4, quindi 4 è la radice quadrata di 16.
4 diviso 2 fa 2, quindi 2 è la radice quadrata di 4.
Trova la radice quadrata di altri numeri
Indovina e poi usa il processo di eliminazione.
Esempio: trova la radice quadrata di 20.
Nel frattempo, sappiamo che 16 è un numero quadrato perfetto con radice quadrata di 4 (4X4=16).
25 ha anche una radice quadrata di 5 (5X5=25).
Quindi supponiamo che la radice quadrata di 20 sia compresa tra 4 e 5.
Possiamo supporre che la radice quadrata di 20 sia 4,5 e provare ad elevare al quadrato 4,5 per verificarlo. Cioè, prendiamo 4,5 x 4,5, se la risposta non è 20, allora vediamo se il risultato è maggiore o minore di 20 per calcolare. Se è inferiore a 20, allora continuiamo a provare con 4, 6 e numeri più grandi. Se il risultato è maggiore di 20, prova a calcolare con 4,4 e numeri più piccoli fino a ottenere il risultato corretto.
Il risultato di questo calcolo è 4,475 X 4,475 = 20,03. Arrotondando per difetto, la risposta è 20.
Come confrontare le radici quadrate
Con 2 numeri positivi qualsiasi a e b
Se a = b allora
Se a > b allora
Se un < b="" allora="">
Per esempio:
Confronta e
Poiché 21 < 31,
Ci auguriamo che l'articolo sopra riportato vi abbia aiutato ad acquisire nozioni sulle radici quadrate, a calcolare, a confrontare... a risolvere esercizi sulle radici quadrate e altri esercizi correlati.