La formula per calcolare l'area e il perimetro di un parallelogramma è una conoscenza di base. Fare riferimento alla formula compilata da Quantrimang.com di seguito.
Sommario
1. Area del parallelogramma
L'area di un parallelogramma si misura in base alla superficie, ovvero la parte piana visibile del parallelogramma.
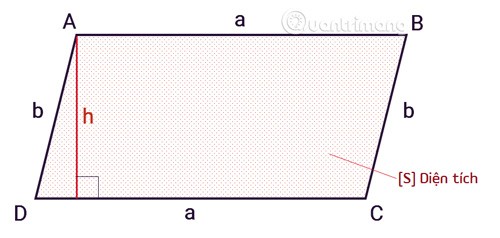
L'area di un parallelogramma si calcola con la formula uguale al prodotto della base per l'altezza.
SABCD = axh
Lì dentro:
Sè l'area di un parallelogramma.aè la base del parallelogramma.hè l'altezza, dalla cima alla base, di un parallelogramma.
2. Perimetro del parallelogramma
Il perimetro di un parallelogramma si calcola sommando la lunghezza delle linee che circondano la figura, che è anche la linea che circonda l'intera area, pari a 2 volte la somma di qualsiasi coppia di lati adiacenti.
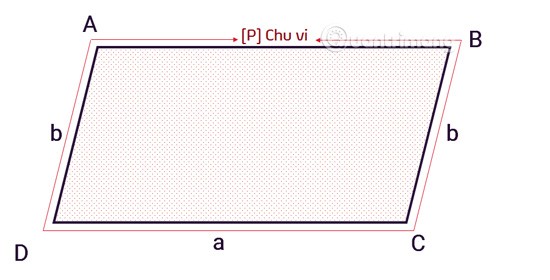
In altre parole, il perimetro di un parallelogramma è la somma delle lunghezze dei quattro lati. La formula specifica è la seguente:
C = 2 x (a+b)
Lì dentro:
Cè il perimetro di un parallelogramma.ae bsono lati adiacenti di un parallelogramma.
3. Che cos'è un parallelogramma?
Definire
Un parallelogramma è un quadrilatero con 2 coppie di lati paralleli oppure 1 coppia di lati paralleli e uguali. Un parallelogramma ha due angoli opposti uguali e due diagonali che si intersecano nel punto medio della figura.
Il parallelogramma può essere considerato un caso speciale di trapezio.
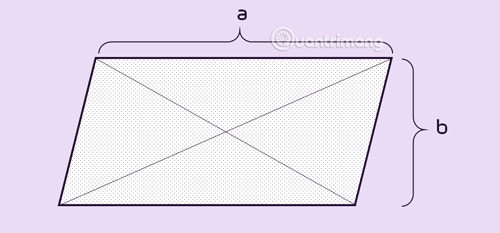
Proprietà del parallelogramma
Nel parallelogramma:
- I lati opposti sono uguali.
- Gli angoli opposti sono uguali.
- Due diagonali si intersecano nel punto medio di ciascuna linea.
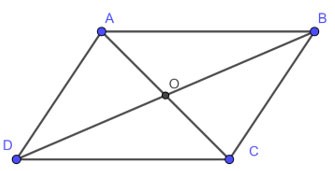
ABCD è un parallelogramma, AC interseca BD in O. Quindi:
• AB = CD, AD = BC
•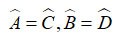
• OA = OC, OB = OD
Segnali di riconoscimento
a) Un quadrilatero con i lati opposti paralleli è un parallelogramma.
b) Un quadrilatero con i lati opposti uguali è un parallelogramma.
c) Un quadrilatero con due lati opposti paralleli e uguali è un parallelogramma.
d) Un quadrilatero con gli angoli opposti uguali tra loro è un parallelogramma.
e) Un quadrilatero con due diagonali che si intersecano nel punto medio di ciascuna è un parallelogramma.
4. Domande a risposta multipla per ripassare i parallelogrammi
Esercizio 1 : Scegli la frase sbagliata.
A. Un parallelogramma ha due diagonali che si intersecano nel punto medio di ciascuna diagonale.
B. Il parallelogramma ha due angoli opposti uguali
C. Un parallelogramma ha due diagonali perpendicolari tra loro.
D. Due parallelogrammi hanno due coppie di lati opposti paralleli.
Soluzione
Nel parallelogramma:
+ Il parallelogramma ha i lati opposti paralleli
+ I lati opposti sono uguali
+ Due diagonali si intersecano nel punto medio di ciascuna linea, quindi C è errata.
La risposta corretta è: C
Esercizio 2 : Dato il parallelogramma ABCD con  = α > 900. All'esterno del parallelogramma, disegna i triangoli equilateri ADE, ABF. Che tipo di triangolo è il triangolo CEF? Scegli la risposta migliore
A. Triangolo
B. Triangolo isoscele
C. Triangolo equilatero
D. Triangolo ottuso
Risposta:
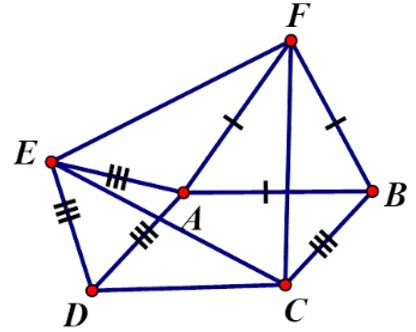

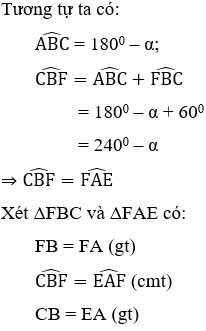
⇒ ΔFBC = ΔFAE (cgc) ⇒ CF = FE (2)
Da (1) e (2) possiamo dedurre che CF = FE = EC, quindi il triangolo CEF è equilatero.
Lezione 3 : Scegli la frase sbagliata. ABCD è un parallelogramma. Poi:
A. AB = CD
B. d.C. = a.C.
C. Test del parallelogramma con risposte
D. AC = BD
Soluzione
Nel parallelogramma:
+ Il parallelogramma ha i lati opposti paralleli
+ I lati opposti sono uguali
+ Due diagonali si intersecano nel punto medio di ciascuna linea, quindi D è errata.
Lezione 4 : Completa lo spazio vuoto con la frase appropriata: "Un quadrilatero con due diagonali... è un parallelogramma".
A. uguale
B. intersecare
C. si intersecano nel punto medio di ogni linea
D. parallelo
Soluzione
Segnali:
Un quadrilatero con due diagonali che si intersecano nel punto medio di ciascuna è un parallelogramma.
Lezione 5 : Scegli la frase sbagliata:
A. Un quadrilatero con due coppie di lati opposti paralleli è un parallelogramma.
B. Un trapezio con due angoli uguali adiacenti a una base è un parallelogramma.
C. Un quadrilatero con due coppie di lati opposti uguali è un parallelogramma.
D. Un quadrilatero con due coppie di angoli opposti uguali è un parallelogramma.
Soluzione
Segnali:
+ Un quadrilatero con lati opposti paralleli è un parallelogramma, quindi A è corretta.
+ Un quadrilatero con lati opposti uguali è un parallelogramma, quindi D è corretta.
+ Un quadrilatero con angoli opposti uguali tra loro è un parallelogramma, quindi D è corretta.
Poiché un trapezio con due angoli uguali adiacenti a una base è un trapezio isoscele, B è sbagliato.
La risposta corretta è: B
5. Esempi di calcolo del perimetro e dell'area del parallelogramma
Esempio 1 : Dato un parallelogramma con base di 12 cm, lato di 7 cm e altezza di 5 cm. Calcola il perimetro e l'area di quel parallelogramma?
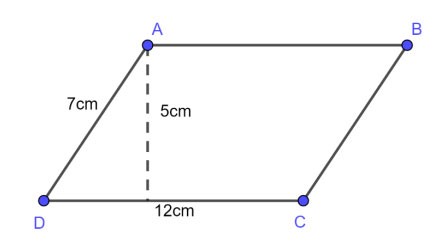
Premio:
Il perimetro del parallelogramma è:
P = 2 x (12 + 7) = 38 (cm)
L'area di un parallelogramma è:
S = axh = 12 x 5 = 60 (cm2)
Esempio 2:
Dato il parallelogramma ABCD, con H e K che sono i piedi delle altezze tracciate rispettivamente dai vertici A, C e BD.
a) Dimostrare che AHCK è un parallelogramma.
b) Sia O il punto medio di HK. Dimostrare che A, O, C sono collineari.
Istruisci:
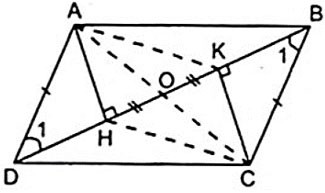
a) Dall'ipotesi abbiamo:
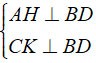 ⇒ AH//CK. ( 1 )
⇒ AH//CK. ( 1 )
Applicando le proprietà dei lati dei parallelogrammi e quelle degli angoli alterni, abbiamo:
 ⇒ Δ ADH = Δ CBK
⇒ Δ ADH = Δ CBK
(caso ipotenusa – angolo acuto)
⇒ AH = CK (i lati corrispondenti sono uguali) ( 2 )
Da (1) e (2) abbiamo che il quadrilatero AHCK con i lati opposti paralleli e uguali è un parallelogramma.
b) Applicare le proprietà delle diagonali del parallelogramma AHCK
Il parallelogramma AHCK ha due diagonali AC e HK che si intersecano nel punto medio di ciascuna retta. Poiché O è il punto medio di HK, O è anche il punto medio di AC.
⇒ A, O, C sono su una linea retta.
Oltre ai parallelogrammi, molto importanti e ampiamente applicate nello studio e nella vita sono anche le formule per calcolare l'area e il perimetro di altre forme geometriche comuni come rombi , quadrati , trapezi , rettangoli ...
Ci auguriamo che attraverso l'articolo sopra riportato abbiate compreso meglio e afferrato le nozioni di base sui parallelogrammi. Se avete domande o commenti da discutere con Quantrimang.com, lasciate un commento qui sotto.




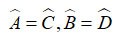



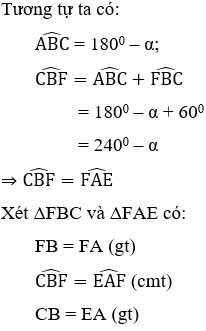


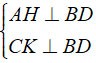 ⇒ AH//CK. ( 1 )
⇒ AH//CK. ( 1 ) ⇒ Δ ADH = Δ CBK
⇒ Δ ADH = Δ CBK