Formula per calcolare larea del rombo, perimetro del rombo

Rivediamo e memorizziamo la formula per calcolare l'area, il perimetro e la diagonale di un rombo nell'articolo seguente.

Sommario

• 1. Formula per calcolare l'area di un rombo
  • Formula per calcolare l'area di un rombo in base alla base e all'altezza
  • Formula per calcolare l'area di un rombo in base alla formula del triangolo (se si conosce l'angolo del rombo)
• 2. Formula per calcolare il perimetro di un rombo
• 3. Che cos'è un rombo?
  • Proprietà del rombo
• 4. Esempio di calcolo dell'area e del perimetro del rombo

1. Formula per calcolare l'area di un rombo

L'area di un rombo si misura in base alla superficie, ovvero la parte piana visibile del rombo.

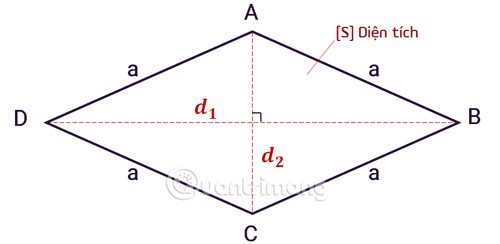
Formula per calcolare l'area di un rombo in base alla base e all'altezza

L'area di un rombo è uguale alla metà del prodotto delle lunghezze delle due diagonali , la formula è la seguente:

Lì dentro:

• Sè l'area del rombo.
• d1e d2sono le due diagonali di un rombo.

Esempio di calcolo dell'area di un rombo.

Lezione 1: C'è un pezzo di cartone a forma di rombo con due diagonali che si intersecano lunghe rispettivamente 6 cm e 8 cm. Qual è l'area del cartone a forma di rombo?

Applicando il metodo di calcolo dell'area di un rombo, abbiamo d1 = 6 cm e d2 = 8 cm. Lo inseriamo nella formula e otteniamo il seguente risultato:

S = 1/2 x (d1 x d2) = 1/2 (6 x 8) = 1/2 x 48 = 24 cm2

Formula per calcolare l'area di un rombo in base alla formula del triangolo (se si conosce l'angolo del rombo)

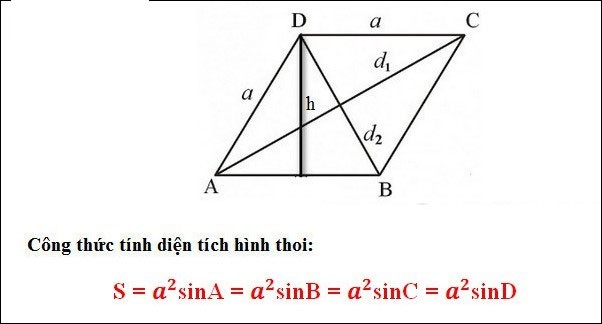
In cui: a: lato del rombo

Esempio 1 : Dato il rombo ABCD, con spigolo = 4 cm, angolo A = 35 gradi. Calcola l'area del rombo ABCD.

Soluzione: applicando la formula, abbiamo a = 4, angolo = 35 gradi. Sostituiamo la formula come segue:

S = a2 x sinA = 42 x sin(35) = 9,176 (cm2)

2. Formula per calcolare il perimetro di un rombo

Il perimetro di un rombo si calcola sommando le lunghezze delle linee che circondano la figura, che è anche la linea che circonda l'intera area.

Per calcolare il perimetro di un rombo, calcoliamo la somma delle lunghezze dei quattro lati. La formula specifica è la seguente:

Lì dentro:

• Pè il perimetro del rombo.
• aè la lunghezza del lato del rombo.

Ad esempio: dato un rombo ABCD con lati uguali e lunghi 7 cm. Qual è il perimetro di questo rombo?

Secondo la formula per calcolare il perimetro di un rombo introdotta sopra, abbiamo a = 7 cm. Pertanto, il perimetro del rombo ABCD verrà calcolato come segue:

P (ABCD) = ax 4 = 7 x 4 = 28 cm

3. Che cos'è un rombo?

Un rombo è un quadrilatero con quattro lati uguali. Si tratta di un parallelogramma con due lati adiacenti uguali oppure di un parallelogramma con due diagonali perpendicolari tra loro.

Proprietà del rombo

• 2 angoli opposti uguali
• 2 diagonali sono perpendicolari tra loro e si intersecano nel punto medio di ciascuna linea
• Le due diagonali sono le bisettrici degli angoli.

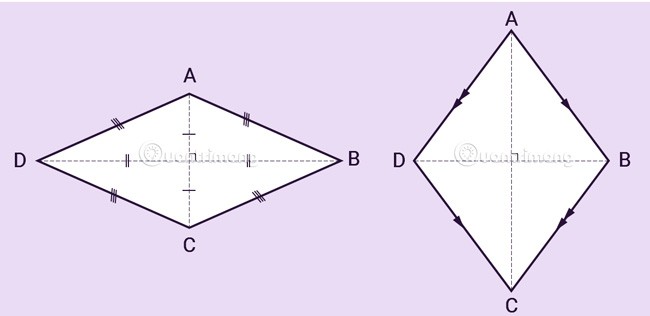
In questo articolo, Quantrimang.com riproporrà formule efficaci per calcolare l'area e il perimetro di un rombo, per i vostri studi e il vostro lavoro.

4. Esempio di calcolo dell'area e del perimetro del rombo

Esempio 1: 

Dato il rombo ABCD con lato AD = 4m, angolo DAB = 30 gradi. Calcola l'area del rombo ABCD.

Premio:

Poiché ABCD è un rombo, i triangoli formati sono triangoli isosceli. Sia I il punto medio delle due diagonali, quindi AI è perpendicolare a BD, angolo IAB = 15 gradi.

Pertanto, AI = AB. cos IAB = 4. Cos 15 = 3,84m.

Considerando il triangolo rettangolo ABI, secondo il teorema di Pitagora, abbiamo:

BI2= AB2- AI2= 1,25 m

Quindi BI = 1,1 m

CA = 2. AI = 7,68 m

BD = 2. BI = 2,2 m

In base alla formula per calcolare l'area di un rombo, abbiamo l'area del rombo ABCD = ½ . Corrente alternata. BD = 8,45(m2)

Esempio 2: Dato un rombo con lato lungo 6 cm e uno dei suoi angoli che misura 60°, calcola l'area del rombo.

Con questi dati non avrai alcuna base per calcolare l'area di un rombo. Per calcolare la diagonale di un rombo sarà necessario basarsi sulle proprietà dei rombi, sulle proprietà dei triangoli equilateri e su come calcolare i lati di un triangolo rettangolo. I passaggi sono i seguenti:

Fase 1: Disegna un'immagine e annota i fatti noti.

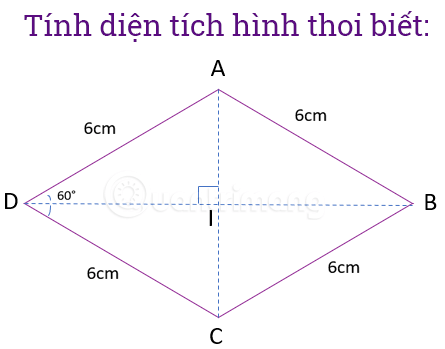
Passaggio 2: Applicando le proprietà di un rombo abbiamo:

, la diagonale AC è la bisettrice dell'angolo A, quindi l'angolo sarà uguale a 1/2 dell'angolo e pari a 60°. (La somma degli angoli interni di un quadrilatero è 360°, la somma degli angoli interni di un triangolo è 180°). Pertanto, il triangolo ADC sarà un triangolo equilatero => il lato AC è 6 cm. I è il punto medio di AC => AI=3cm.

Passaggio 3: calcolare la lunghezza di DI

Il triangolo DIA è rettangolo in I, il lato DI verrà calcolato come segue:

=> cm

Passaggio 4: Calcola l'area del rombo ABCD:

Esempio 3: Dato un rombo ABCD con lato lungo 13 cm, due diagonali si intersecano in H.

Calcola l'area del rombo ABCD sapendo che BH è una volta e mezzo AH.

Soluzione:

ABCD è un rombo, quindi AH è perpendicolare a BH in H, quindi il triangolo ABH è rettangolo in H.

Sia BH = 2a, allora AH = 3a.

Secondo il teorema di Pitagora abbiamo: AH²+ BH²= AB² ⇒9a²+4a²=13 ⇒13a²=13 ⇒a=1

Pertanto AH = 3 cm, BH = 2 cm o AC = 6 cm, BD = 4 cm

L'area del rombo è: S = 6,4/2= 12cm².

Esempio 4 :

Dato il rombo MNPQ, angolo A = 30o, perimetro = 20m, il punto medio della diagonale è I. Qual è l'area del rombo MNPQ?

Soluzione

La lunghezza del lato del rombo è a = P : 4 = 20 : 4 = 5m

Poiché i triangoli creati dai rombi sono tutti triangoli isosceli, il triangolo creato dal punto medio della diagonale I, punti M, N sarà creato dall'angolo IMN = 15o

Lunghezza della mezza diagonale MI = MN x cos IMN = 5 x cos150 = 4,8 m

Applicando il teorema di Pitagora al triangolo rettangolo MNI abbiamo: NI = 1,4m

Lunghezza diagonale NQ = 2 x NI = 2 x 1,4 = 2,8 m

L'area del rombo MNPQ è S = 2 x ½ x NQ x MI = 1 x ½ x 2,8 x 4,8 = 13,44 m2

Risposta: 13,44 m2

Se avete domande sulla formula per calcolare l'area e il perimetro di un rombo, lasciate un commento qui sotto per discuterne e rispondere insieme. Grazie per aver seguito l'articolo.