Formula per calcolare laltezza nei triangoli regolari, isosceli, equilateri e rettangoli

L'altezza in un triangolo è una linea retta con proprietà importanti ed è strettamente correlata ai problemi di geometria piana. Quindi, qual è l'altezza? Come si calcola l'altezza di un triangolo? Per la risposta e la formula più semplice per calcolare l'altezza di un triangolo, fare riferimento all'articolo seguente.

Sommario

• Formula per calcolare l'altezza in un triangolo
  • Calcola l'altezza in un triangolo regolare
  • Calcola l'altezza in un triangolo equilatero
  • Formula per calcolare l'altezza in un triangolo rettangolo
  • Formula per calcolare l'altezza in un triangolo isoscele
• Definizione di altezza in un triangolo
• Proprietà delle tre altezze di un triangolo

Formula per calcolare l'altezza in un triangolo

Calcola l'altezza in un triangolo regolare

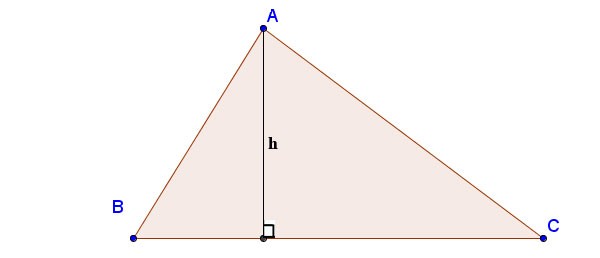
Come calcolare l'altezza di un triangolo usando la formula di Erone:

Essendo a, b, c le lunghezze dei lati; ha è l'altitudine tracciata dal vertice A al lato BC; p è il semiperimetro:

Per esempio: 

Dato il triangolo ABC, lato AB = 4 cm, lato BC = 7 cm, lato AC = 5 cm. Calcola l'altitudine AH dall'intersezione di A con BC in H e calcola l'area di ABC.

Premio:

Semiperimetro del triangolo: P = (AB + BC + AC) : 2 = (4 + 7 + 5) : 2 = 8(cm)

Altezza   

=>

Consideriamo il triangolo ABC, abbiamo:

COSÌ,

Calcola l'altezza in un triangolo equilatero

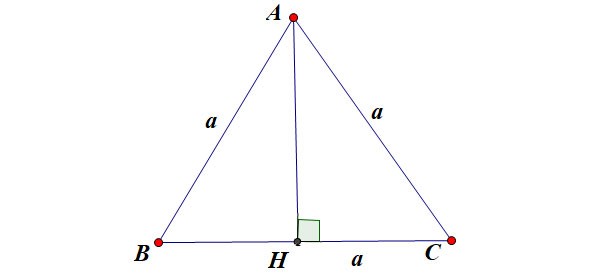
Supponiamo che il triangolo equilatero ABC abbia il lato di lunghezza a come mostrato in figura:

Lì dentro:

• h è l'altezza di un triangolo equilatero
• a è la lunghezza del lato di un triangolo equilatero

Formula per calcolare l'altezza in un triangolo rettangolo

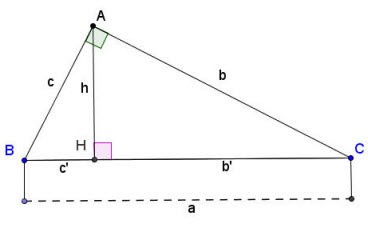
Supponiamo che ci sia un triangolo rettangolo ABC retto in A come mostrato sopra:

Formula per calcolare i lati e le altezze di un triangolo rettangolo:

1. a2 = b2 + c2

2. b2 = ab′ e c2 = ac′

3. ah = bc

4. h2 = b′.c'

5.

Lì dentro:

• a, b, c sono i lati di un triangolo rettangolo come mostrato sopra;
• b' è la proiezione del lato b sull'ipotenusa;
• c' è la proiezione del lato c sull'ipotenusa;
• h è l'altezza di un triangolo rettangolo tracciato dal vertice dell'angolo retto A fino all'ipotenusa BC.

Esempio 1: Dato il triangolo ABC rettangolo in A, altezza AH. Calcola BC, AC, AH sapendo che AB = 15 cm, HC = 16 cm.

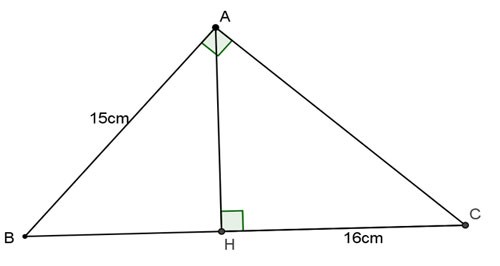
Premio:

Applicando la formula algebrica al triangolo rettangolo ABC abbiamo:

AC2 = CH.BC = 16.BC

Secondo il teorema di Pitagora per il triangolo rettangolo ABC con angolo retto A abbiamo:

AB2 + AC2 = BC2

⇔ 152 + 16.a.C. = a.C.2

⇔ aC2 - 16 aC - 225 = 0

⇔ aC2 - 25 aC + 9 aC - 225 = 0

⇔ BC(BC - 25) + 9(BC - 25) = 0

⇔ (BC - 25)(BC + 9) = 0

⇔ BC = 25 o BC = -9 (elimina)

⇒ AC2 = 16.BC = 16,25 = 400 ⇒ AC = 20 (cm)

Consideriamo il triangolo rettangolo ABC con: AH.BC = AB.AC (formula geometrica)

=> AH = AB.AC/BC = 15.20/25 = 12(cm)

Quindi BC=25(cm); CA=20(cm); AH=12(cm)

Esempio 2 :

Dato il triangolo ABC, questo è rettangolo in A, AB=24cm, AC=32cm. La bisettrice di BC interseca AC, BC rispettivamente in D ed E. Calcola DE.

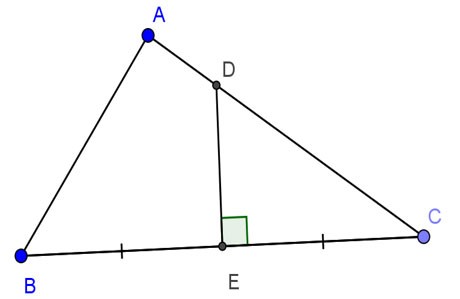
Premio:

Considerando il triangolo rettangolo ABC, abbiamo:

BC2 = AB2 + AC2 (secondo il teorema di Pitagora)

BC2 = 242+ 322

BC2 = 1600

BC = 40(cm)

CE = BC : 2 = 40 : 2 = 20(cm)

Consideriamo il triangolo rettangolo ACB e il triangolo rettangolo ECD con:

C'è ∠A = ∠E = 90o

∠C comune

=> Triangolo ACB ∾ triangolo ECD (gg)

=> AC/EC = AB/ED

=> ED = AB.EC/AC = 15cm

Quindi ED = 15 cm

Formula per calcolare l'altezza in un triangolo isoscele

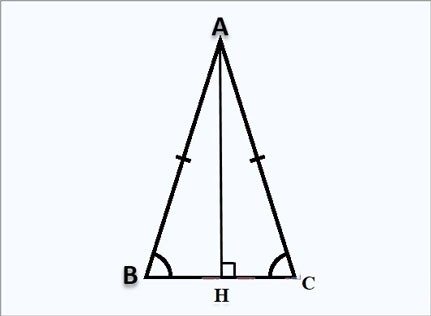
Supponiamo di avere un triangolo isoscele ABC in A, l'altezza AH è perpendicolare a H come mostrato sopra:

Formula per calcolare l'altezza AH:

Poiché il triangolo ABC è isoscele in A, l'altezza AH è anche la mediana, quindi:

⇒ HB=HC= ½BC

Applicando il teorema di Pitagora al triangolo rettangolo ABH retto in H abbiamo:

AH²+BH²=AB²

⇒AH²=AB²−BH²

Ad esempio : dato Δ ABC è in equilibrio in A con BC = 30(cm), altezza AH = 20(cm). Calcola l'altezza corrispondente al lato di quel triangolo isoscele.

Soluzione: considera che Δ ABC è isoscele in A con BC = 30(cm)

⇒ BH = CH = 15(cm).

Applicando il teorema di Pitagora abbiamo:

Adesso dobbiamo calcolare BK = ?

Abbiamo:

D'altra parte

Pertanto, abbiamo ⇔

Definizione di altezza in un triangolo

L'altezza di un triangolo è un segmento perpendicolare che va da un vertice al lato opposto. Questo lato opposto è chiamato base e corrisponde all'altitudine. La lunghezza dell'altitudine è la distanza tra la cima e il fondo.

Proprietà delle tre altezze di un triangolo

Le tre altezze di un triangolo passano per lo stesso punto. Quel punto è chiamato ortocentro del triangolo .

Per poter calcolare l'altezza di un triangolo è sufficiente calcolare i componenti sconosciuti nelle formule sopra riportate per calcolare l'altezza di un triangolo.

• Qual è il fulcro? Formula per calcolare il baricentro di un triangolo