Formula per calcolare la diagonale di un rombo

Un rombo è un quadrilatero con quattro lati uguali, un quadrilatero con due diagonali perpendicolari tra loro nel punto medio di ciascuna retta è un rombo, un parallelogramma con due lati adiacenti uguali... Oltre a quadrati, rettangoli, triangoli... il rombo è una delle forme geometriche importanti nella matematica e nella vita.

Oltre alla formula per calcolare il perimetro e l'area di un rombo , è molto importante anche il modo per calcolare la diagonale di un rombo, ovvero la linea che collega tra loro i vertici opposti del rombo.

L'articolo seguente ti aiuterà a imparare come calcolare la diagonale di un rombo con esempi specifici; fai riferimento ad esso.

Sommario

• Diagonale di un rombo
• Proprietà delle diagonali di un rombo
• Formula per calcolare la diagonale di un rombo
• Problema sul calcolo della diagonale del rombo

Diagonale di un rombo

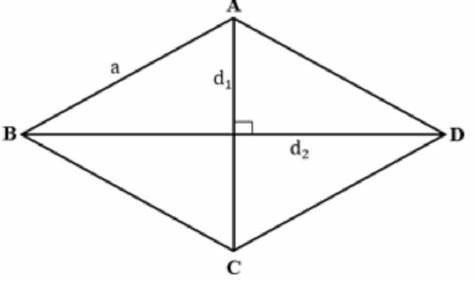
• La diagonale di un rombo è la linea che collega due vertici opposti del rombo.
• Un rombo ha due diagonali, che si intersecano nel punto medio del rombo.
• La diagonale divide il rombo in due triangoli equilateri con lati uguali.

Proprietà delle diagonali di un rombo

Le due diagonali di un rombo hanno le seguenti proprietà:

• Due diagonali uguali: le due diagonali di un rombo sono di uguale lunghezza.
• L'angolo tra due diagonali è un angolo retto: le due diagonali di un rombo si intersecano nel punto medio del rombo e formano un angolo retto.
• Le diagonali sono gli assi di simmetria di un rombo: ogni diagonale di un rombo è un asse di simmetria del rombo, che divide il rombo in due metà simmetriche.
• Le diagonali sono le diagonali di due triangoli equilateri: ogni diagonale di un rombo è una diagonale di due triangoli equilateri, formati da lati uguali.
• Il prodotto delle lunghezze delle due diagonali è uguale al prodotto delle lunghezze dei due lati di un rombo: Il prodotto delle lunghezze delle due diagonali è uguale al prodotto delle lunghezze dei due lati di un rombo. Cioè, se indichiamo la diagonale con d e i lati con a e b, abbiamo d² = a² + b².

Queste proprietà sono caratteristiche dei rombi e vengono utilizzate in molti problemi geometrici che li riguardano.

Formula per calcolare la diagonale di un rombo

Per ricavare la formula per calcolare la diagonale di un rombo, si consideri l'esempio seguente.

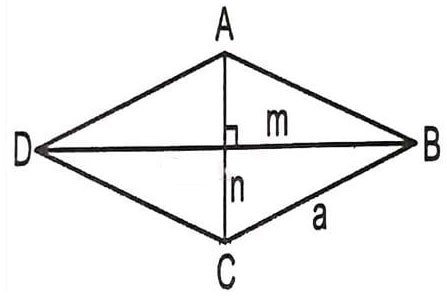
Supponiamo di dover calcolare la lunghezza della diagonale di un rombo ABCD con lato a e angolo ABC = 60 gradi -> qual è la formula per calcolare la diagonale di un rombo in questo caso?

Soluzione:

Poiché ABCD è un rombo, tutti i lati sono uguali ad a.

Consideriamo il triangolo ABC con: AB = BC = a

Ancora: ABC = 60 gradi => Il triangolo ABC è un triangolo equilatero con lato a.

=> AB = AC = BC = a

=> La lunghezza della diagonale del rombo è AC = BD = a.

La soluzione sopra riportata è una delle formule più semplici e facili da capire per calcolare la diagonale di un rombo.

Formula per calcolare la diagonale di un rombo conoscendo l'area e la diagonale rimanente

Dalla formula per calcolare l'area di un rombo:

S = (axb) : 2

La formula per la lunghezza della diagonale è la seguente:

a = S x 2 : b

O

b = S x 2 : a

Lì dentro:

• S è l'area
• a e b sono le lunghezze delle due diagonali

Utilizzare le proprietà geometriche di un rombo per calcolare la lunghezza della diagonale senza ricorrere al teorema di Pitagora. Nello specifico:

La diagonale di un rombo è la media delle due altezze.

Diagonale = radice quadrata di (altezza lunga + altezza corta)²

La diagonale di un rombo è la metà del perimetro del rombo.

Diagonale = 1/2 x perimetro del rombo.

Problema sul calcolo della diagonale del rombo

Problema 1: Dato un rombo con area di 360 centimetri quadrati e diagonale lunga 24 centimetri. Calcola la lunghezza della seconda diagonale

Soluzione:

Secondo la formula per l'area di un rombo: axb : 2

Abbiamo la seconda diagonale: 360 x 2 : 24 = 30 cm

Risposta: 30 cm

Problema 2:

Un rombo ha un'area di 4 dm, la lunghezza di una diagonale è 3/5 dm. Calcola la lunghezza della seconda diagonale. Soluzione:

La lunghezza della seconda diagonale è:

(4 x 2) : 3/5 = 40/3 (dm)

Lezione 3: Le due diagonali di un rombo sono lunghe 160 cm e 120 cm. Calcola l'altezza del rombo, sapendo che il rapporto tra l'altezza e la lunghezza del lato del rombo è 24:25.

Soluzione:

L'area del rombo è: 160,120:2 = 9 600 (cm2).

Poiché il rapporto tra l'altezza e la lunghezza del lato di un rombo è 24:25, possiamo considerare l'altezza del rombo 24a e il lato 25a.

Abbiamo quindi l'area del rombo: 25a,24a = 9 600 a2 = 16 a = 4 cm.

L'altezza del rombo è: 24,4 = 96 (cm).

Quindi l'altezza del rombo è 96 cm.

Lezione 4: 

Dato il rombo ABCD con lato lungo 12,5 cm, altezza lunga 6,72 cm e AC più piccolo di BD. Quali sono rispettivamente le lunghezze delle diagonali AC e BD?

Premio:

Applica la formula per calcolare l'area di un rombo: S = ha = 6,72 x 12,5 = 84 cm.
=> 1/2 AC x BD = 84 => 2AC.BD = 336

Sia O l'intersezione delle due diagonali di un rombo.

Abbiamo AOB è un triangolo rettangolo in O quindi AB2 = OA2 + OB2

In cui, OA = 1/2 AC, OB = 1/2 BD

=> 12,52 = 1/4 (AC2 + BD2) <=> 625 = AC2 + BD2

AC2 + BD2 = 625 <=> AC2 + BD2+ 2AC.BD = 625 + 336 <=> (AC + BD)2 = 961 <=> AC + BD = 31 (1)

AC2 + BD2 = 625 <=> AC2 + BD2- AC.BD = 625 -336 <=> (BD - AC)2 = 289 <=> BD - AC = 17 (Secondo il problema BD > AC) (2)

Da (1) e (2), abbiamo:

BD = 24, AC = 7 cm.

Lezione 5: 

Il rombo ABCD ha i lati pari a 10 unità. Calcola la lunghezza della diagonale del rombo.

Soluzione: La lunghezza della diagonale del rombo ABCD è:

Diagonale = radice quadrata di 2(10²) = radice quadrata di 200 = 14,14 unità di lunghezza.

Quindi la lunghezza della diagonale del rombo ABCD è 14,14 unità di lunghezza.

Lezione 6:

Il rombo ABCD ha una diagonale di 12 unità. Calcola il perimetro del rombo.

Soluzione: Poiché un rombo ha quattro lati uguali, il suo perimetro sarà la somma delle lunghezze dei quattro lati, ovvero:

Perimetro = 4 x lunghezza del lato = 4 x 6 = 24 unità di lunghezza.

Quindi il perimetro del rombo ABCD è 24 unità di lunghezza.