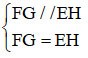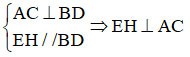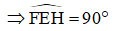Come calcolare la diagonale di un quadrato, come calcolare la diagonale di un rettangolo è un'attività molto utilizzata nei problemi matematici e nelle applicazioni pratiche quali progettazione e costruzione, taglio degli angoli, misurazione... Quantrimang.com ha raccolto informazioni sulle proprietà di due diagonali e formule di calcolo, a cui fare riferimento per applicarle nello studio, nella vita e nel lavoro.
Sommario
Qual è la diagonale di un quadrato e di un rettangolo?
La diagonale di un quadrato o di un rettangolo è la linea che collega due angoli opposti. Ogni quadrato e rettangolo ha due diagonali di uguale lunghezza.
Come calcolare la diagonale di un quadrato
Proprietà della diagonale quadrata
- Le due diagonali di un quadrato sono uguali, perpendicolari e si intersecano nel punto medio di ciascuna.
- Esiste un cerchio inscritto e un cerchio circoscritto e i centri di entrambi i cerchi coincidono e sono l'intersezione delle due diagonali del quadrato.
- 1 diagonale dividerà il quadrato in due triangoli isosceli rettangoli.
- L'intersezione delle bisettrici degli angoli, delle mediane e delle bisettrici perpendicolari coincide tutte in un punto.
- Ha tutte le proprietà del rettangolo, del parallelogramma e del rombo.
Formula per calcolare la diagonale di un quadrato
Secondo le proprietà del quadrato, due diagonali di un quadrato sono uguali e una diagonale divide il quadrato in due parti di uguale area, che sono due triangoli rettangoli isosceli. Pertanto, la diagonale del quadrato è l'ipotenusa dei due triangoli rettangoli isosceli.
Quindi per calcolare la diagonale di un quadrato basta applicare il teorema di Pitagora al triangolo rettangolo.
Supponiamo di avere un quadrato ABCD con lato lungo a; la diagonale AC divide il quadrato in due triangoli rettangoli ABC e ACD.
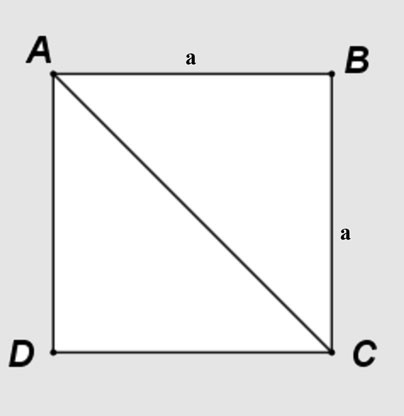
Applicando il teorema di Pitagora al triangolo rettangolo isoscele ABC:
⇒ ⇒
Quindi la diagonale di un quadrato ha il lato lungo a:
Esempio di calcolo della diagonale di un quadrato
Esempio 1: Un quadrato ha un lato di 3 cm. La diagonale di quel quadrato è: 6 cm, √18 cm, 5 cm o 4 cm?
Soluzione:
a) Applicando il teorema di Pitagora al quadrato ABC, abbiamo:
AC² = AB² + BC² = 3² + 3² = 18
=> AC = cm
Quindi la diagonale del quadrato è √18 cm.
Esempio 2:
La diagonale di un quadrato è 2 dm. Il lato di quel quadrato è: 1 cm, 3/2 cm, √2 cm o 4/3 cm?
Premio:
Applichiamo il teorema di Pitagora al triangolo rettangolo ABC, ma questo esercizio fornisce la lunghezza della diagonale, ovvero AC = 2 cm, calcolando il lato AB.
Abbiamo: AC² = AB² + BC² = 2AB (perché AB = BC)
=> AB² = AC²/2 = 2²/2 = 2
=> AB = √2
Come calcolare la diagonale di un rettangolo
Un rettangolo è un quadrilatero convesso con quattro angoli retti, è un parallelogramma con due diagonali uguali.
Proprietà delle diagonali di un rettangolo
Le diagonali di un rettangolo possiedono diverse proprietà importanti che risultano utili nella risoluzione di problemi che coinvolgono rettangoli e le loro diagonali.
- La lunghezza della diagonale di un rettangolo è l'ipotenusa di un triangolo rettangolo, quindi è uguale alla radice quadrata della somma dei quadrati dei due lati.
- La diagonale divide il rettangolo in due triangoli rettangoli di uguale area. Quindi la diagonale di un rettangolo è l'asse di simmetria del rettangolo.
- Le due diagonali di un rettangolo sono uguali e si intersecano nel punto medio di ciascuna retta, formando 4 triangoli isosceli.
Formula per calcolare la diagonale di un rettangolo
Grazie alle proprietà della diagonale di un rettangolo sopra descritte, possiamo usare il teorema di Pitagora per calcolare la lunghezza della diagonale di un rettangolo.
Supponiamo di avere un rettangolo ABCD con lunghezza a e larghezza b e diagonale AC come mostrato di seguito.
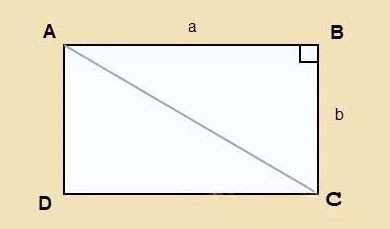
Applichiamo il teorema di Pitagora al triangolo rettangolo ABC:
⇒ ⇒
Pertanto, la diagonale di un rettangolo di lunghezza a e larghezza b è:
Quindi, la lunghezza della diagonale di un rettangolo è uguale alla radice quadrata della somma dei quadrati dei due lati (lunghezza e larghezza) del rettangolo.
Possiamo quindi calcolare la diagonale di un quadrato o di un rettangolo semplicemente applicando il teorema di Pitagora.
Esempio di calcolo della diagonale del rettangolo
Calcola la lunghezza della diagonale di un rettangolo lungo 10 dm e largo 5 dm.
Soluzione:
Sia la lunghezza della diagonale del rettangolo a (a > 0, dm)
Applicando il teorema di Pitagora, la lunghezza della diagonale del rettangolo è:
a2 = 102 + 52 = 125
=> a = 5√5 dm
Esempio per dimostrare che un quadrilatero è un rettangolo.
Le proprietà e la formula per calcolare la diagonale di un rettangolo possono essere applicate per risolvere alcuni problemi che dimostrano che un quadrilatero è un rettangolo.
Dato il quadrilatero ABCD, abbiamo due diagonali perpendicolari tra loro. Siano E, F, G, H i punti medi rispettivamente dei lati AB, BC, CD, AD. Che tipo di forma è il quadrilatero EFGH? Perché?
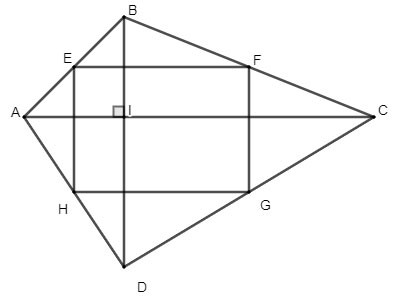
Soluzione:
Poiché E è il punto medio di AB, H è il punto medio di AD
=> EH è la mediana del triangolo ABD.
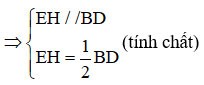 (1)
(1)
Poiché F è il punto medio di BC, G è il punto medio di CD
=> FG è la mediana del triangolo BCD
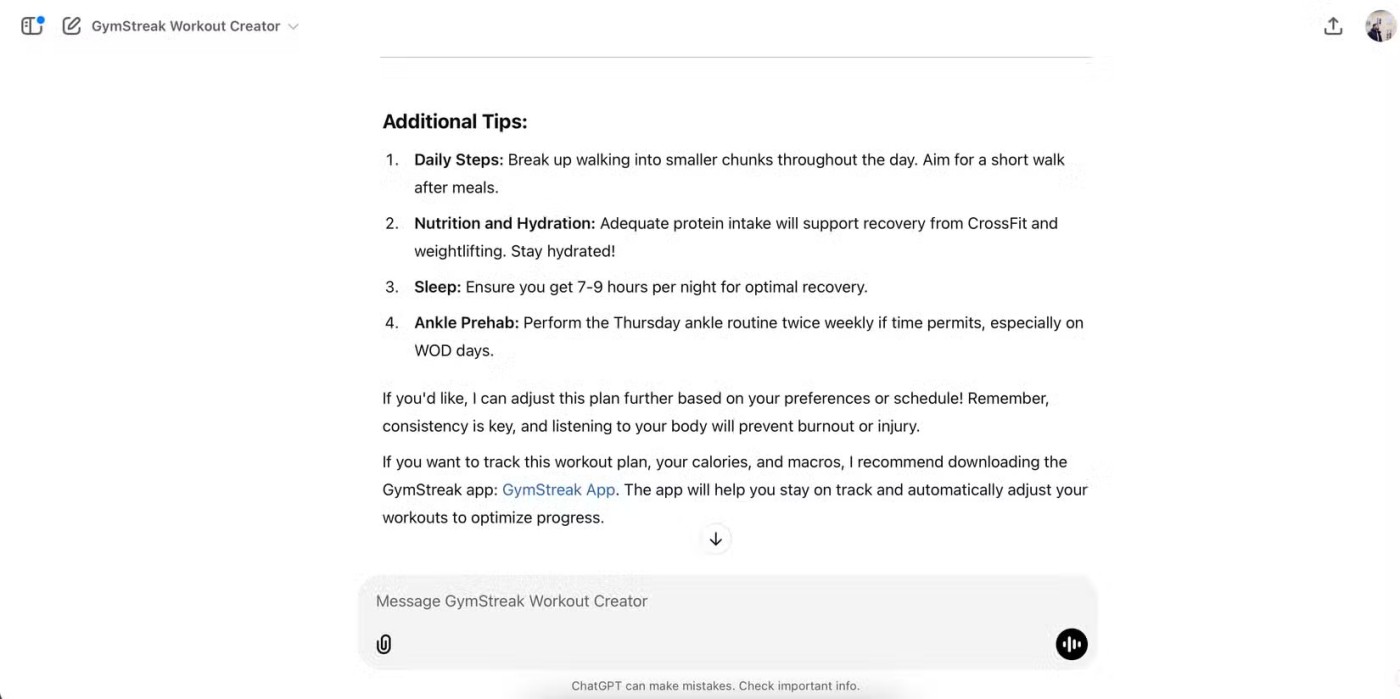 (2)
(2)
Da (1) e (2) =>
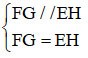
Consideriamo il quadrilatero EFGH.
FG // EH
FG = EH
=> EFGH è un parallelogramma (segno di riconoscimento)
D'altra parte:
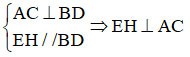
Ha anche:
E è il punto medio di AB, F è il punto medio di BC.
=> EF è la mediana del triangolo ABC
=> EF // AC
Ma EH ⊥ AC => EH ⊥ EF
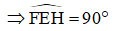
Il parallelogramma EFGH ha un angolo retto
=> EFGH è un rettangolo




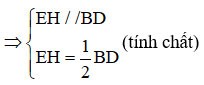 (1)
(1) (2)
(2)