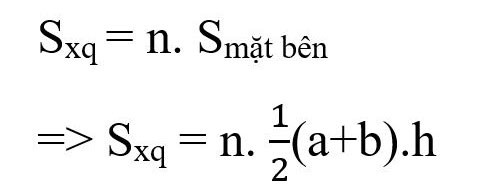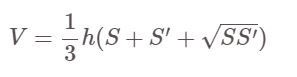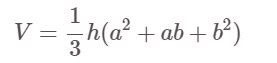Nell'articolo seguente impareremo cos'è una piramide tronca, come calcolare il volume di una piramide tronca, l'area laterale e l'area totale di una piramide tronca.
Sommario
Definizione di tronco
Una piramide tronca è una parte di un poliedro, situata tra la base e la sezione trasversale tagliata da un piano parallelo alla base della piramide.
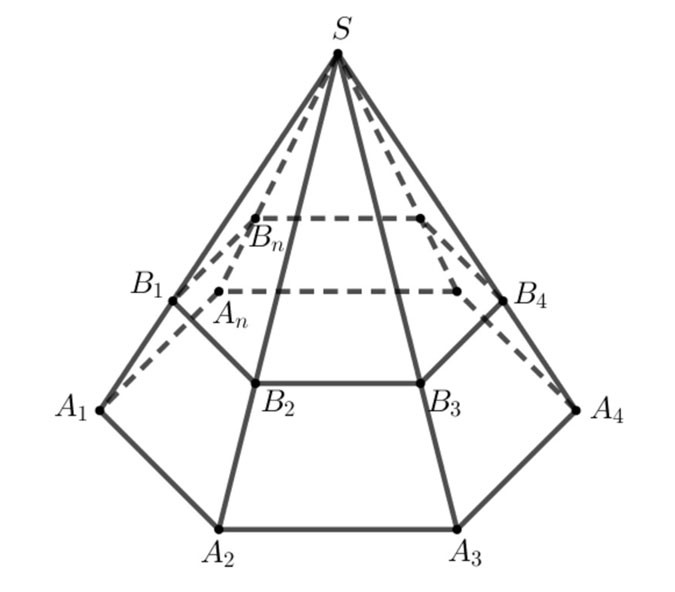
- La figura composta dai poligoni A1A2...An,B1B2...BnA1A2...An,B1B2...Bn e dai trapezi A1A2B2B1,A2A3B3B2,...,AnA1B1BnA1A2B2B1,A2A3B3B2,...,AnA1B1Bn è chiamata piramide tronca, indicata con A1A2...An.B1B2...Bn.A1A2...An.B1B2...Bn.
- In parole povere, una piramide tronca è formata dalla piramide S.A1A2...AnS.A1A2...An dopo aver tagliato la piramide S.B1B2...Bn.S.B1B2...Bn.
+ I poligoni A1A2...An,B1B2...BnA1A2...An,B1B2...Bn sono chiamati le due basi,
+ I trapezi A1A2B2B1,A2A3B3B2,...,AnA1B1BnA1A2B2B1,A2A3B3B2,...,AnA1B1Bn sono chiamati facce laterali.
+ I segmenti di linea A1B1,A2B2,...,AnBnA1B1,A2B2,...,AnBn sono detti spigoli laterali, gli spigoli della superficie di base sono detti spigoli di base.
+ La distanza tra le due basi è chiamata altezza della piramide tronca.
Proprietà della piramide tronca:
- Le due basi sono due poligoni (triangoli, quadrilateri, pentagoni, ecc.) con lati paralleli corrispondenti e rapporti uguali tra i lati corrispondenti.
- Le facce laterali sono tutte trapezie.
- Le linee che contengono i bordi laterali convergeranno in un punto (la sommità della piramide).
- Una piramide tronca è una piramide le cui basi sono poligoni regolari (con lati uguali). Pertanto, le facce laterali di un tronco di cono sono tutte trapezi uguali.
Formula per calcolare l'area di una piramide tronca
Area superficiale della piramide tronca
L'area laterale di una piramide tronca è l'area delle facce circostanti, la parte che circonda la piramide tronca, escludendo l'area delle due basi.
Come calcolare l'area laterale di una piramide tronca: calcola l'area di ciascuna faccia laterale (trapezi) della piramide tronca secondo la formula per il calcolo dell'area di un trapezio normale , quindi calcola l'area totale.
Formula per calcolare l'area di una piramide tronca regolare:
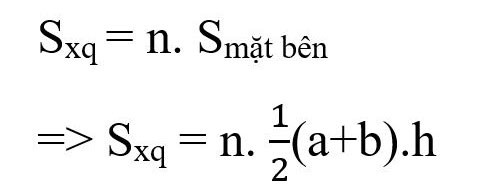
Lì dentro:
- Sxq: area circostante
- n: numero di facce laterali della piramide tronca (uguale al numero di spigoli del poligono di base)
- a, b: lunghezze laterali rispettivamente delle basi superiore e inferiore
- h: altezza dei quadrilateri laterali.
Esempio 1:
Calcola l'area laterale di una piramide tronca quadrilatera regolare con spigoli di base di 10 cm e 15 cm e altezza laterale di 12 cm.

Premio:
La faccia laterale di una piramide tronca quadrilatera regolare è un trapezio isoscele, quindi l'area di una faccia laterale è:
Una piramide tronca quadrilatera regolare ha 4 lati uguali, quindi la sua area laterale è:
150 x 4 = 600 (cm2)
Esempio 2: Calcola l'area laterale di una piramide tronca quadrilatera regolare con spigoli di base di 6 cm e 8 cm e altezza laterale di 5 cm. Calcola l'area laterale di una piramide tronca quadrilatera regolare con spigoli di base di 6 cm e 8 cm.

Premio:
La faccia laterale di una piramide tronca quadrilatera regolare è un trapezio isoscele, quindi l'area di una faccia laterale è uguale a
Una piramide tronca quadrilatera regolare ha quattro lati uguali quindi la sua area laterale è uguale a
35 x 4 = 140 (cm2)
Superficie totale di una piramide tronca
L'area totale di una piramide tronca è uguale alla somma dell'area laterale e dell'area delle due basi.
Formula: Stp = Sxq + Fondo grande + Fondo piccolo
Lì dentro:
- Stp: Area totale
- Sxq: Area circostante
- Base grande: ampia area di base
- Base piccola: Area di base piccola
Per esempio:
Calcola l'area totale di una piramide tronca regolare in base alle dimensioni indicate in figura.
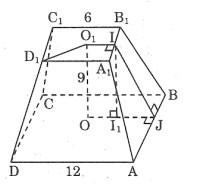
Premio:
Abbiamo:
AD = 12 ⇒ GU = 6
Disegna II1 ⊥ OJ abbiamo: I1J = 3
Applicando il teorema di Pitagora al triangolo rettangolo II1J abbiamo:
IJ2 = II12 + I1J2 = 92 + 32 = 90
Quindi:
L'area di un lato di un trapezio è:
L'area circostante è pari a:
L'area della base superiore è: S = 6 x 6 = 36 (unità)
L'area della base inferiore è: S = 12 x 12 = 144 (unità)
L'area totale di una piramide tronca è uguale a:
Formula per calcolare il volume di una piramide tronca
Ricetta:
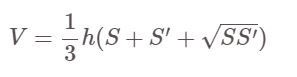
Lì dentro:
- V: volume della piramide tronca
- S, S' sono rispettivamente le aree della base grande e piccola della piramide.
- h: altezza della piramide, cioè la distanza tra le due basi grande e piccola
Una piramide tronca è un quadrato (un quadrilatero regolare):
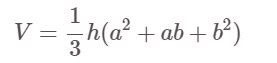
Lì dentro:
- V: Volume
- h: Altezza della piramide
- a, b sono rispettivamente le lunghezze dei bordi della base grande e della base piccola.