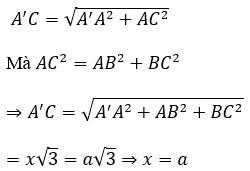Un prisma è un poligono con due basi parallele e uguali e le facce laterali a parallelogramma.
Commento:
- Le facce laterali di un prisma sono uguali e parallele tra loro.
- Le facce laterali sono parallelogrammi.
- Le due basi di un prisma sono due poligoni uguali.
Qual è la formula per calcolare il volume di un prisma (prisma V) e qual è la formula per calcolare il volume di un prisma verticale? Fare riferimento all'articolo qui sotto.
Sommario
1. Volume di un prisma verticale
Formula per calcolare il volume di un prisma verticale:
Il volume di un prisma retto è uguale al prodotto dell'area della base per l'altezza.
Lì dentro
Vè il volume del prisma (unità m3)Bè l'area di base (unità m2)hè l'altezza del prisma (unità m)
3. Classificazione dei prismi
Prisma regolare
È un prisma verticale con base poligonale regolare. Le facce laterali del prisma sono tutte rettangoli uguali. Ad esempio: prisma triangolare regolare, quadrilatero regolare... allora lo intendiamo come prisma regolare.
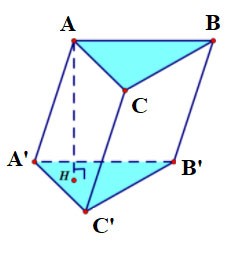
Una base quadrilatera regolare è chiamata prisma quadrilatero regolare.
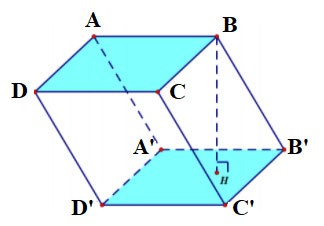
Prisma triangolare
- Un prisma triangolare ha 5 facce, 9 spigoli e 6 vertici.
- Le due basi sono entrambe triangolari e parallele tra loro; Ogni faccia laterale è un rettangolo;
- I lati sono uguali;
- L'altezza di un prisma triangolare è la lunghezza di un lato.
Per esempio:
Il prisma triangolare ABC.A'B'C' ha:
- La base inferiore è il triangolo ABC, la base superiore è il triangolo A'B'C';
Le facce laterali sono rettangoli: AA'B'B, BB'C'C, CC'A'A;
- Bordi:
- Bordi di base: AB, BC, CA, A'B', B'C', C'A'
- Lati: AA', BB', CC';
- Vertici: A, B, C, A', B', C'.
- L'altezza è la lunghezza di un lato: AA' o BB' o CC'.
Prisma quadrilatero
- Un prisma quadrilatero ha 6 facce, 12 spigoli e 8 vertici.
- Le due basi sono entrambe quadrilatere e parallele tra loro. Ogni faccia laterale è un rettangolo.
- I lati sono uguali.
- L'altezza di un prisma quadrilatero è la lunghezza di un lato.
Per esempio:
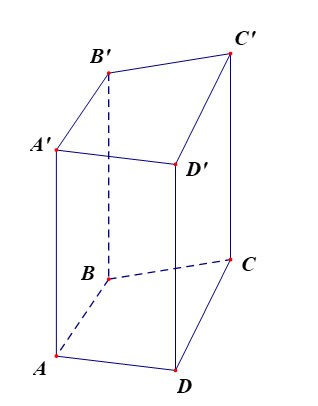
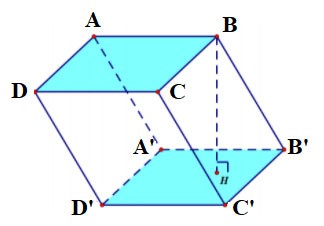
Il prisma quadrilatero ABCD.A'B'C'D' ha:
- La base inferiore è il quadrilatero ABCD, la base superiore è il quadrilatero A'B'C'D';
Le facce laterali sono rettangoli: AA'B'B, BB'C'C, CC'D'D, DD'A'A;
- Bordi:
+ Bordi di base: AB, BC, CD, DA, A'B', B'C', C'D', D'A'
+ Bordi laterali: AA', BB', CC', DD' sono uguali.
- Vertici: A, B, C, D, A', B', C', D'.
- L'altezza è la lunghezza di un lato: AA' o BB' o CC' o DD'.
Nota: anche i prismi rettangolari e i cubi sono prismi quadrilateri.
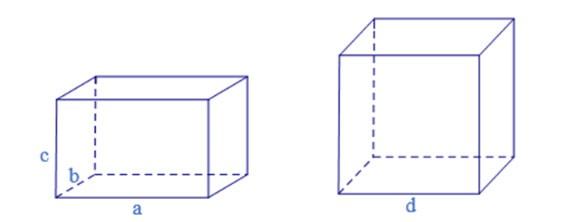
Prisma retto
Se un prisma ha gli spigoli laterali perpendicolari alla base, si dice prisma retto.
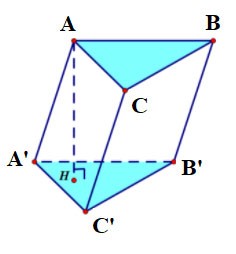
Nota:
Se la base è un rettangolo, il cilindro verticale del quadrilatero è chiamato scatola rettangolare.
Se un cilindro quadrilatero ha 12 lati di lunghezza a, allora il suo nome è cubo.
Confronta il prisma retto e il prisma normale:
| DEFINIRE: |
NATURA |
| + Un prisma verticale è un prisma con un lato perpendicolare alla base. |
+ Le facce laterali di un prisma verticale sono rettangolari.
+ Le facce laterali del prisma sono perpendicolari alla faccia di base.
+ L'altezza è il lato
|
| + Un prisma regolare è un prisma verticale la cui base è un poligono regolare. |
+ Le facce laterali di un prisma sono tutte rettangoli uguali.
+ L'altezza è il lato
|
4. Esempio di calcolo del volume di un prisma verticale
Esempio 1:
Dato il prisma ABC.A'B'C' con base ABC pari a un triangolo equilatero con lato a = 2 cm e altezza h = 3 cm. Calcola il volume di questo prisma?
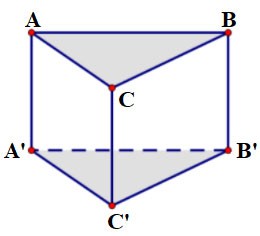
Premio:
Poiché la base è un triangolo equilatero di lato a, l'area è:
In questo momento, il volume del prisma è:
Esempio 2:
Esercizio 1: Dato un parallelepipedo verticale con spigoli AB = 3a, AD = 2a, AA' = 2a. Calcola il volume del blocco A'.ACD'
Istruisci:
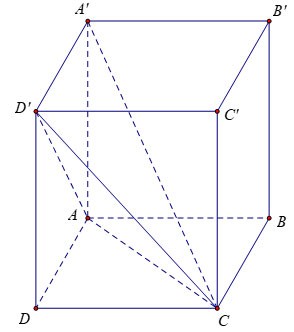
Poiché la faccia laterale ADD'A' è un rettangolo, abbiamo:
Esempio 3 : Dato un prisma verticale ABC.A'B'C' la cui base è un triangolo equilatero di lato a√3, l'angolo tra la base e il prisma è di 60º. Sia M il punto medio di BB'. Calcola il volume della piramide M.A'B'C'.
Premio:
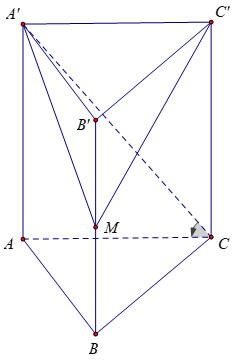
Pertanto, possiamo dedurre che
Abbiamo:
Esempio 4:
Dato un prisma quadrilatero regolare ABCD.A'B'C'D' con uno spigolo di base di lunghezza a e una faccia (DBC') che forma un angolo di 60º con la base ABCD. Calcola il volume del prisma ABCD.A'B'C'D?
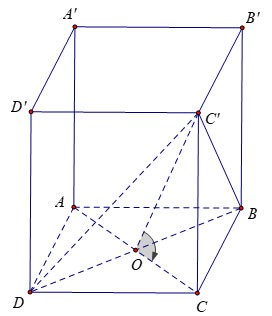
Abbiamo: al centro O del quadrato ABCD.
D'altra parte quindi
Dedurre
Anche:
Esempio 5:
Calcola il volume V del cubo ABCD.A'B'C'D', sapendo AC'=a√3
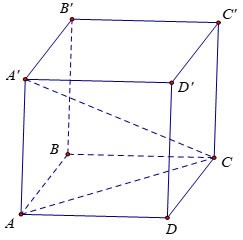
Premio:
Sia x la lunghezza del lato del cubo.
Consideriamo il triangolo AA'C rettangolo in A con:
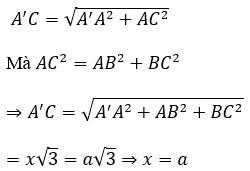
Pertanto, il volume del cubo è V=a^3.
Oltre alla formula per calcolare il volume di un prisma riportata sopra, puoi consultare altri articoli sulla formula per calcolare il volume di un solido di rotazione , sulla formula per calcolare l'area e la circonferenza di un cerchio ...