Sistemi esadecimali e decimali
L'esadecimale ha 16 cifre. Le cifre da 1 a 9 sono le stesse del sistema decimale, poi i numeri decimali da 10 a 15 sono sostituiti dalle lettere A, B, C, D, E ed F dell'alfabeto inglese.
Il sistema decimale (noto anche come sistema base 10) è il sistema standard per la rappresentazione dei numeri interi e non interi (numeri decimali). Si tratta di un'estensione per i numeri non interi del sistema numerico indo-arabico.
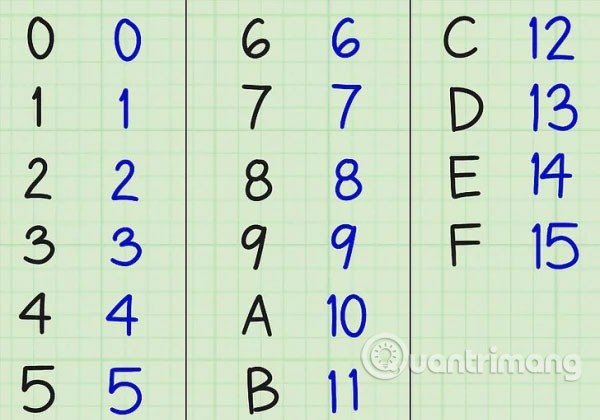
Come convertire la base 16 in base 10
Il sistema esadecimale è un sistema numerico a base 16, mentre il sistema decimale è un sistema numerico a base 10. A volte abbiamo bisogno di conoscere l'equivalente decimale di un numero esadecimale.
Ecco i passaggi per convertire dalla base 16 alla base 10:
Ecco un esempio:
7DE è un numero esadecimale
7DE = 2014 (in decimale)
Esempio di conversione dalla base 16 alla base 10:
Tabella di conversione da base 16 a base 10
| Sistema esadecimale | Sistema base 10 |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| UN | 10 |
| B | 11 |
| C | 12 |
| D | 13 |
| E | 14 |
| F | 15 |
Vedi anche:
In questo articolo ti guideremo su come recuperare l'accesso al tuo disco rigido in caso di guasto. Seguici!
A prima vista, gli AirPods sembrano identici a qualsiasi altro auricolare true wireless. Ma tutto è cambiato quando sono state scoperte alcune caratteristiche poco note.
Apple ha presentato iOS 26, un importante aggiornamento con un nuovissimo design in vetro smerigliato, esperienze più intelligenti e miglioramenti alle app più note.
Gli studenti hanno bisogno di un tipo specifico di portatile per i loro studi. Non solo deve essere abbastanza potente da essere adatto al corso di laurea scelto, ma anche compatto e leggero da poter essere portato con sé tutto il giorno.
Aggiungere una stampante a Windows 10 è semplice, anche se la procedura per i dispositivi cablati sarà diversa da quella per i dispositivi wireless.
Come sapete, la RAM è una componente hardware molto importante in un computer: funge da memoria per l'elaborazione dei dati ed è il fattore che determina la velocità di un laptop o di un PC. Nell'articolo seguente, WebTech360 vi illustrerà alcuni metodi per verificare la presenza di errori nella RAM utilizzando un software su Windows.
Le smart TV hanno davvero preso d'assalto il mondo. Grazie alle sue numerose funzionalità e alla connettività Internet, la tecnologia ha cambiato il nostro modo di guardare la TV.
I frigoriferi sono elettrodomestici comuni nelle case. I frigoriferi hanno solitamente 2 scomparti: lo scomparto freddo è spazioso e ha una luce che si accende automaticamente ogni volta che l'utente lo apre, mentre lo scomparto congelatore è stretto e non ha luce.
Oltre ai router, alla larghezza di banda e alle interferenze, le reti Wi-Fi sono influenzate da molti fattori, ma esistono alcuni modi intelligenti per potenziare la propria rete.
Se vuoi tornare alla versione stabile di iOS 16 sul tuo telefono, ecco la guida di base per disinstallare iOS 17 ed effettuare il downgrade da iOS 17 a 16.
Lo yogurt è un alimento meraviglioso. Fa bene mangiare yogurt tutti i giorni? Se mangiassi yogurt ogni giorno, come cambierebbe il tuo corpo? Scopriamolo insieme!
In questo articolo vengono illustrati i tipi di riso più nutrienti e come sfruttare al massimo i benefici per la salute offerti dal tipo di riso scelto.
Tra le misure che possono aiutarti a dormire meglio e a svegliarti puntuale al mattino c'è quella di stabilire un orario per dormire e una routine per andare a dormire, cambiare la sveglia e modificare la tua dieta.
Affitto per favore! Landlord Sim è un gioco di simulazione per dispositivi mobili, disponibile per iOS e Android. Giocherai nei panni del proprietario di un complesso di appartamenti e inizierai ad affittare un appartamento con l'obiettivo di migliorarne gli interni e prepararli per gli inquilini.
Ottieni il codice del gioco Roblox Bathroom Tower Defense e riscattalo per ottenere fantastiche ricompense. Ti aiuteranno a potenziare o sbloccare torri con danni maggiori.
