Che cosa è un numero reale?

Cosa sono i numeri reali? Quali numeri appartengono all'insieme dei numeri reali? Per comprendere meglio questa importante conoscenza matematica, vi invitiamo a leggere l'articolo qui sotto.

Numero reale

• 1. Che cos'è un numero reale?
• 2. Asse dei numeri reali
•  3. Confronta i numeri reali
• 3. Proprietà dell'insieme dei numeri reali
• 4. Valore assoluto di un numero reale
• 5. Esercizi di esempio sui numeri reali

1. Che cos'è un numero reale?

• I numeri reali sono l'insieme dei numeri razionali e dei numeri irrazionali.
• Insieme è il simbolo dell'insieme dei numeri reali, costituito dai numeri reali.

• Un numero razionale è un numero scritto come frazione (a, b ∈ Z, b ≠ 0). Per esempio 
• L'insieme dei numeri razionali è indicato da 
• Un numero irrazionale è un numero decimale infinito e non periodico. Per esempio:
• L'insieme dei numeri irrazionali è indicato con 

L'insieme dei numeri reali copre la retta numerica.

Per esempio:

2. Asse dei numeri reali

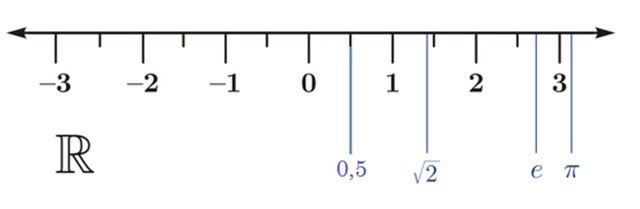
Ogni numero reale è rappresentato da un punto sulla retta numerica.

• Al contrario, ogni punto sulla retta numerica rappresenta un numero reale.
• Solo l'insieme dei numeri reali riempie la retta numerica.

 3. Confronta i numeri reali

Metodo

• Con due numeri reali qualsiasi x, y, abbiamo sempre x = y o x < y o x > y
• I numeri reali maggiori di 0 sono detti numeri reali positivi, mentre i numeri reali minori di 1 sono detti numeri reali negativi. Il numero 0 non è né un numero reale positivo né negativo.
• Il confronto tra numeri reali positivi è simile al confronto tra numeri razionali.
• Essendo a, b due numeri reali positivi, se a > b allora .

Esempio: inserisci la cifra appropriata nel quadrato:

Guida alle soluzioni

a) -7,5(0)8 > -7,513

b) -3,02 <>

c) -0.4(9)854 <>

d) -1,(9)0765 <>

Esempio: Disporre i numeri reali: in ordine dal più piccolo al più grande

Guida alle soluzioni

Disporre i numeri reali dal più piccolo al più grande:

Ad esempio: dimostrare che:

Con a, b sono due numeri reali positivi se a > b allora

Guida alle soluzioni

Se a > b allora

a, b sono due numeri reali positivi quindi a + b > 0

Se a > b allora a – b > 0

Considera il prodotto

Poiché a2 – b2 > 0

=> a2 > b2 => dpcm

3. Proprietà dell'insieme dei numeri reali

Nell'insieme definiamo anche le operazioni di addizione, sottrazione, moltiplicazione, divisione, elevamento a potenza, radici quadrate... E nelle operazioni i numeri reali hanno anche le stesse proprietà delle operazioni nell'insieme dei numeri razionali.

Nell'insieme dei numeri reali, le operazioni hanno le seguenti proprietà rispetto alla moltiplicazione:

• Per tutte le proprietà:
• Aggiungi 0: 
• Proprietà commutativa: ;
• Proprietà combinate: 
• Proprietà commutativa: a. b = b. UN
• Proprietà associative: (a. b). c = a. (b. c)
• Proprietà della moltiplicazione per 1:
• Proprietà distributiva della moltiplicazione rispetto all'addizione: a. (b + c) = a. b + a. C
• Per ogni numero reale a ≠ 0, esiste un inverso tale che

- Vale a dire che anche i calcoli sopra riportati hanno proprietà commutative e associative come altri insiemi di numeri. E lo stesso vale per sottrazione, moltiplicazione, divisione…

Relazione tra insiemi di numeri

Ad esempio: eseguire il calcolo:

Guida alle soluzioni

Ad esempio: Trova x, sapendo:

Guida alle soluzioni

4. Valore assoluto di un numero reale

Definizione: La distanza dal punto a al punto 0 sulla retta numerica è il valore assoluto di un numero a (a è un numero reale). Il valore assoluto di un numero negativo è se stesso, il valore assoluto di un numero negativo è il suo opposto.

Panoramica:

• Se
• Se
• Se
• Se

Natura

• Il valore assoluto di ogni numero è non negativo.
• Generale: per ogni a ∈ R

Nello specifico:

Alcune proprietà

- Due numeri uguali o opposti hanno lo stesso valore assoluto e viceversa, due numeri che hanno lo stesso valore assoluto sono uguali o opposti.

Panoramica:

- Ogni numero è maggiore o uguale al suo opposto del valore assoluto e allo stesso tempo minore o uguale al suo valore assoluto.

Panoramica: e

- Di due numeri negativi, il più piccolo ha valore assoluto maggiore.

Panoramica: Se

- Di due numeri positivi, il più piccolo ha il valore assoluto più piccolo.

Panoramica: Se

- Il valore assoluto di un prodotto è uguale al prodotto dei valori assoluti.

Panoramica:

- Il valore assoluto di un quoziente è uguale al quoziente di due valori assoluti.

Panoramica:

5. Esercizi di esempio sui numeri reali

Esempio 1: Completa gli spazi vuoti con i simboli appropriati ∈, ∉, ⊂ (…):

3 …. Q; 3 …. R ; 3… Io ; -2,53… D;

0,2(35) …. IO ; N …. Z ; IO …. R.

Istruire

a) 3 ∈ Q ; 3 ∈ R ; 3 ∉ Io ; -2,53 ∈ Q

b) 0,2(35) ∉ I ; N ∈ Z ; Io ⊂ R

Esempio 2: Trova gli insiemi

a) Q ∩ I ;
b) R ∩ I.

Istruire

a) Q ∩ I = Ø ;
b) R ∩ I = I.

Esempio 3: Inserisci la cifra appropriata in (…) 

a) – 3.02 < –="" 3,="" …="">

b) – 7,5 … 8 > – 7,513

c) – 0,4 … 854 < –="">

d) -1, … 0765 < –="">

Istruire

a) – 3,02 < –="">
b) – 7.508 > – 7.513 ;
c) – 0,49854 < –="" 0,49826="">
d) -1,90765 < –="">

Esempio 4: Trova x, sapendo:

3,2.x + (-1,2).x +2,7 = -4,9;

Istruire

3.2. x + (-1,2).x + 2,7 = -4,9

[3,2 + (-1,2)].x + 2,7 = -4,9.

2.x + 2,7 = – 4,9.

2.x = – 4,9 – 2,7

2.x = – 7,6

x = -7,6 : 2

x = -3,8

Oltre ai numeri reali, puoi approfondire altre definizioni matematiche, come numeri quadrati , numeri irrazionali, numeri razionali , numeri primi , numeri naturali ...