Impariamo la formula per calcolare l'area laterale, l'area totale e l'altezza di un cilindro da applicare nello studio e nella vita quotidiana.
Sommario
Come calcolare l'area di un cilindro
L'area di un cilindro comprende l'area laterale e l'area totale.
È possibile inserire l'altezza e il raggio del cilindro nella tabella sottostante per conoscere l'area laterale e l'area totale del cilindro.
Formula per calcolare l'area laterale di un cilindro
L'area laterale di un cilindro comprende solo l'area della superficie circostante il cilindro, esclusa l'area delle due basi.
La formula per calcolare l'area laterale di un cilindro è la circonferenza del cerchio di base moltiplicata per l'altezza.
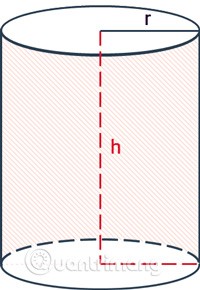 |
Lì dentro:
- I dintorni sono le zone circostanti.
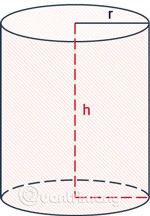
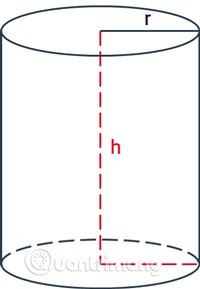
rè il raggio del cilindro.hè l'altezza, la distanza tra le due basi del cilindro.
|
Esempio: 1
Un cilindro circolare ha raggio di base r = 5 cm e altezza h = 7 cm. Calcola l'area laterale di un cilindro verticale.
Soluzione: Area superficiale di un cilindro circolare: Sxq = 2.π.rh = 2π.5.7 = 70π = 219.8 (cm2).
Esempio: 2
Dato il quadrato ABCD di lato 2a. Siano O e O' i punti medi rispettivamente dei lati AB e CD. Ruotando il quadrato attorno all'asse OO', otteniamo un cilindro rotante. Calcola l'area superficiale del cilindro rotante.
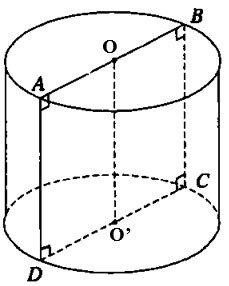
Soluzione:
Il raggio del cerchio di base è r= CD= a
L'altezza del cilindro è h= OO'= AD=2a
Quindi l'area laterale del cilindro è Sxq = 2πrh = 2π.a.2a =4a2π
Formula per calcolare l'area totale di un cilindro
L'area totale si calcola come la grandezza dell'intero spazio occupato dalla figura, compresa l'area laterale e l'area delle due basi circolari.
La formula per calcolare l'area totale di un cilindro è la somma dell'area laterale e dell'area delle due basi.
Esempio 1 : Calcola l'area totale di un cilindro con base 3 e altezza 5.
Soluzione:
L'area totale è Stp = Sxq + 2Sd = 2πr(r+h) = 2π.3(3+5) =48π
Calcola l'altezza del cilindro
L'altezza di un cilindro è la distanza tra le due basi del cilindro.
Calcola l'altezza di un cilindro conoscendo l'area totale e il raggio di base
Ad esempio: dato un cilindro con raggio di base R = 8 cm e area totale 564π cm2. Calcola l'altezza del cilindro.
Premio:
Abbiamo
Calcola l'altezza di un cilindro conoscendo l'area laterale
=>
Formula per calcolare il raggio della base di un cilindro
1. Formula per calcolare la circonferenza di un cerchio; area del cerchio
Il cerchio ha circonferenza C=2πr
=>
Il cerchio di base ha area S=πr2
=>
Per esempio. Calcola il raggio della base del cilindro nei seguenti casi:
UN. La circonferenza del cerchio di base è 6π
B. L'area della base è 25π
Soluzione:
UN. Il raggio del cerchio di base è
B. Il raggio del cerchio di base è
2. La base è il cerchio inscritto nel poligono
- Inscritto in un triangolo qualsiasi: essendo S l'area del triangolo e p il semiperimetro
- Inscritto in un triangolo equilatero: lato
- Quadrato inscritto:
Esempio 1 . Dato un cilindro inscritto in un cubo di spigolo a. Calcola il raggio di quel cilindro.
Il raggio del cilindro è:
Esempio 2 . Dato un prisma regolare ABC.A'B'C' con , il volume circoscritto al cilindro. Calcola il raggio di quel cilindro.
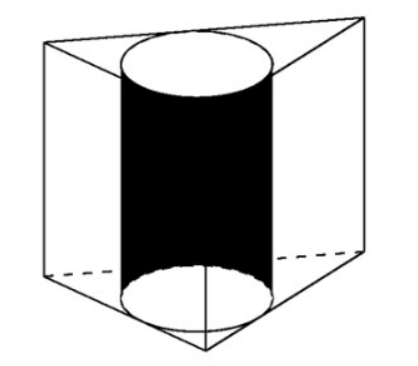
Il volume del prisma è
La base di un prisma regolare è un triangolo equilatero, quindi => il lato
Pertanto, il raggio della base del cilindro è:
3. La base è il cerchio che circoscrive il poligono.
Circoscritto a un triangolo qualsiasi:
Lì dentro:
- a, b, c sono le lunghezze dei tre lati del triangolo
- p è il semiperimetro del triangolo:
Circonferenza di un triangolo rettangolo: ipotenusa
Periferia del triangolo equilatero: lato
Circonferenza del quadrato: lato
Per esempio:
Calcola il raggio di base del cilindro che circoscrive la piramide regolare S.ABC nei seguenti casi:
UN. ABC è un triangolo rettangolo in A con AB = a e AC = a√3
B. ABC ha AB= 5; CA= 7; aC=8
Premio:
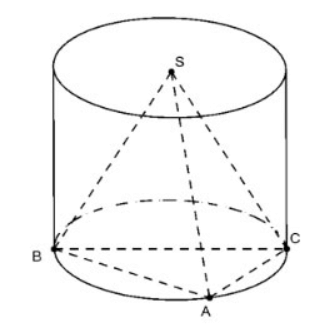
UN. Ipotenusa
Poiché ABC è un angolo retto in A, raggio R=0,5.BC=a
B. Il semiperimetro del triangolo ABC è
Cos'è un cilindro circolare?
Un cilindro circolare è un cilindro con due basi circolari uguali e parallele tra loro.
I cilindri sono usati abbastanza comunemente nei problemi di geometria, da quelli più semplici a quelli più complessi, nei quali la formula per calcolare l'area e il volume dei cilindri è spesso utilizzata in modo diverso. Se sai già come calcolare l'area e la circonferenza di un cerchio, puoi facilmente dedurre le formule per calcolare il volume, l'area laterale e l'area totale di un cilindro.
Formula per calcolare l'area della sezione trasversale di un cilindro
Tagliare il cilindro lungo il piano (P) attraverso l'asse
- La sezione trasversale risultante è un rettangolo.
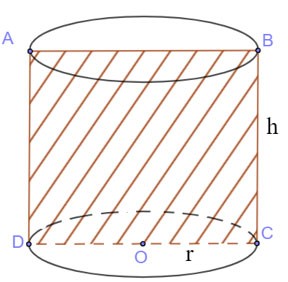 |
Area della sezione trasversale:
SABCD = BC.CD =2r.h
|
Tagliare il cilindro lungo il piano (P) parallelo all'asse e distante x dall'asse
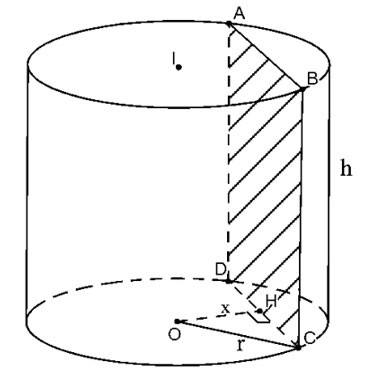 |
La sezione trasversale risultante è il rettangolo ABCD, come mostrato sopra.
Sia H il punto medio di CD, abbiamo OH ⊥ CD=>
Pertanto l'area della sezione trasversale
|
Tagliare il cilindro con un piano (P) non perpendicolare all'asse ma tagliare tutte le generatrici del cilindro
 |
La sezione trasversale formata è un cerchio con centro O' e raggio O'A'=r
Area della sezione trasversale: S= πr2
|
Tagliare il cilindro lungo il piano (P) non perpendicolare all'asse ma tagliare tutte le generatrici del cilindro.
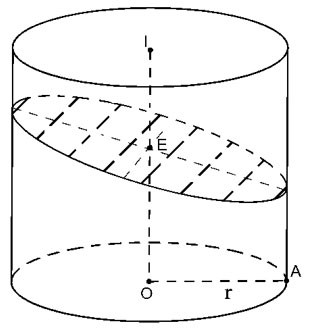 |
La sezione trasversale risultante è un'ellisse (E) con asse minore 2r => a=r
L'asse grande è uguale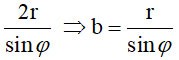
con 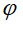 è l'angolo tra l'asse OI e (P) è l'angolo tra l'asse OI e (P)
Quindi area S= π. ab=
|
Esempio di calcolo dell'area di un cilindro
Lezione 1 :
L'area laterale di un cilindro ha una circonferenza di base circolare di 13 cm e un'altezza di 3 cm.
Premio:
Abbiamo: circonferenza del cerchio C = 2R.π = 13cm, h = 3cm
Quindi l'area laterale del cilindro è:
Sxq = 2πr.h = Ch = 13,3 = 39 (cm²)
Lezione 2 : Dato un cilindro con raggio di base di 6 cm, mentre l'altezza dalla base alla sommità del cilindro è di 8 cm di spessore. Quali sono l'area laterale e l'area totale del cilindro?
Premio
Secondo la formula, abbiamo il semicerchio di base r = 6 cm e l'altezza del cilindro h = 8 cm. Pertanto, abbiamo la seguente formula per calcolare l'area laterale di un cilindro e l'area totale di un cilindro:
Area superficiale del cilindro = 2 x π xrxh = 2 x π x 6 x 8 = ~ 301 cm²
Area totale del cilindro = 2 Π x R x (R + H) = 2 X π x 6 x (6 + 8) = ~ 527 cm²
Lezione 3 : Un cilindro ha un raggio di base di 7 cm e un'area laterale di 352 cm2.
Quindi, l'altezza del cilindro è:
(A) 3,2 centimetri; (B) 4,6 centimetri; (C) 1,8 centimetri
(D) 2,1 cm; (E) Un altro risultato
Seleziona il risultato corretto.
Soluzione: abbiamo
Quindi la risposta E è corretta.
Lezione 4 : L'altezza di un cilindro è uguale al raggio del cerchio di base. La superficie laterale del cilindro è di 314 cm2. Calcola il raggio del cerchio di base e il volume del cilindro (arrotonda il risultato a due cifre decimali).
Premio:
L'area laterale del cilindro è di 314 cm2
Abbiamo Sxq = 2.π.rh = 314
Dove r = h
Quindi 2πr² = 314 => r² ≈ 50 => r ≈ 7,07 (cm)
Volume del cilindro: V = π.r2.h = π.r3 ≈ 1109,65 (cm³).
Ci auguriamo che l'articolo sopra riportato vi abbia aiutato ad acquisire conoscenze di base e avanzate sui cilindri e a calcolare l'area totale e l'area laterale di un cilindro.










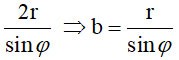
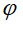 è l'angolo tra l'asse OI e (P)
è l'angolo tra l'asse OI e (P)